Hyperbolic paraboloidΒΆ

Given hyperbolic paraboloid

f(x,y) = x^2-y^2

define corresponding Python function f()

>>> def f(x, y):
        return x ** 2 - y ** 2

Evaluate f() on 100 x 100 uniformly spaced samples in [-1, 1] x [-1, 1].

>>> import numpy as np
>>> t = np.linspace(-1.0, 1.0, 100)
>>> x, y = np.meshgrid(t, t)
>>> z = f(x, y)

Concatenate x, y and z into a single array of points.

>>> P = np.stack([x, y, z], axis=-1).reshape(-1, 3)

Visualize.

>>> import pptk
>>> v = pptk.viewer(P)
>>> v.attributes(P[:, 2])  # color points by their z-coordinates
>>> v.set(point_size=0.005)

One can also calculate and visualize additional per-point attributes.

>>> # calculate gradients
>>> dPdx = np.stack([np.gradient(x, axis=1), np.gradient(y, axis=1), np.gradient(z, axis=1)], axis=-1)
>>> dPdy = np.stack([np.gradient(x, axis=0), np.gradient(y, axis=0), np.gradient(z, axis=0)], axis=-1)

>>> # calculate gradient magnitudes
>>> mag = np.sqrt(np.sum(dPdx ** 2 + dPdy ** 2, axis=-1)).flatten()

>>> # calculate normal vectors
>>> N = np.cross(dPdx, dPdy, axis=-1)
>>> N /= np.sqrt(np.sum(N ** 2, axis=-1))[:, :, None]
>>> N = N.reshape(-1, 3)

>>> # set per-point attributes
>>> v.attributes(P[:, 2], mag, 0.5 * (N + 1))

Toggle between attributes using the [ and ] keys.

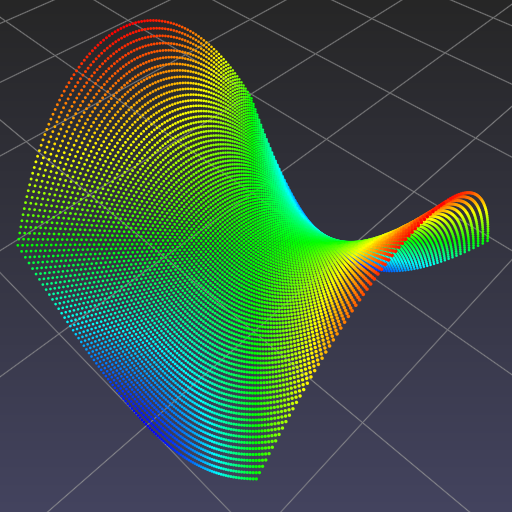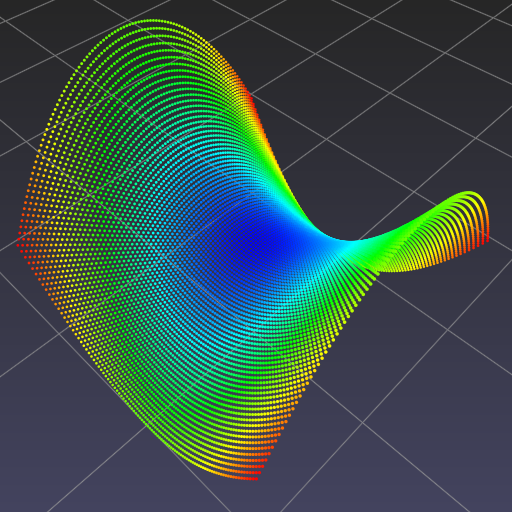saddle_z saddle_mag saddle_n
Visualization of f(x,y)=x^2-y^2. Points are colored by f (left), |\nabla f| (middle), and normal directions (right)