Mobius stripΒΆ

Given the following parametrization of a Mobius strip

x(s,t) & = \left(1+\frac{t}{2}\cos\left(\frac{s}{2}\right)\right)\cos(s) \\ y(s,t) & = \left(1+\frac{t}{2}\cos\left(\frac{s}{2}\right)\right)\sin(s) \\ z(s,t) & = \frac{t}{2}\sin\left(\frac{s}{2}\right)

where 0\le s\le 2\pi and -1\le t\le 1.

Define uniformly spaced samples in parameters s and t.

>>> import numpy as np
>>> s = np.linspace(0.0, 2 * np.pi, 1000)[None, :]
>>> t = np.linspace(-1.0, 1.0, 50)[:, None]

Evaluate the above parametric equations using parameter samples s and t.

>>> x = (1 + 0.5 * t * np.cos(0.5 * s)) * np.cos(s)
>>> y = (1 + 0.5 * t * np.cos(0.5 * s)) * np.sin(s)
>>> z = 0.5 * t * np.sin(0.5 * s)
>>> P = np.stack([x, y, z], axis=-1)

Calculate normals.

>>> N = np.cross(np.gradient(P, axis=1), np.gradient(P, axis=0))
>>> N /= np.sqrt(np.sum(N ** 2, axis=-1))[:, :, None]

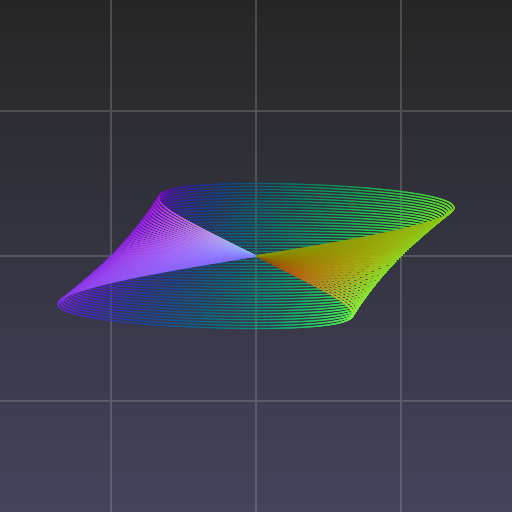
Visualize.

>>> import pptk
>>> v = pptk.viewer(P)
>>> v.attributes(0.5 * (N.reshape(-1, 3) + 1))
>>> v.set(point_size=0.001)
mobius mobius_x mobius_y mobius_z
Visualization of a mobius strip using pptk.viewer(). Points are colored by normal directions. And the latter three images are views along the -x, +y and -z directions.